티스토리 뷰
** 투상에서 사선의 오묘함 (2) - 사선과 원통의 만남
도면에서 사선이 나오면 우선 긴장을 하게 된다. 3D에서는 확인이 가능하지만 막상 정면도, 평면도, 측면도를 그릴려고 하면 무엇인가 맞지 않게 되기 때문이다.
하지만 너무 겁먹지는 말자.
나름 찾는 공식이 있는것 같으니까 말이다.
우선 다음 그림을 확인해보자.
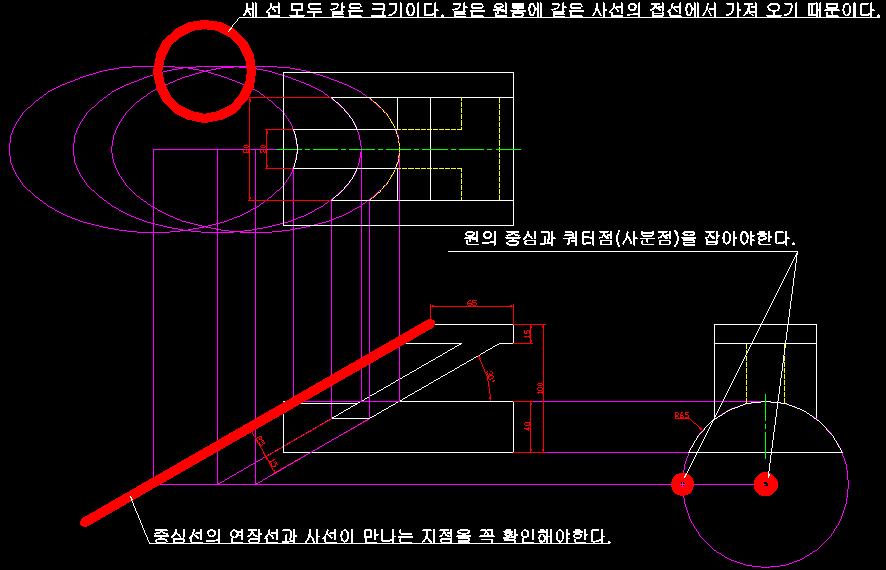
이 그림을 보면 먼가 떠오는 것이 있을 것이다.
바로 사선과 원통의 만남이다. 그것도 원통의 중심이 어긋나서 밖으로 나가 있는 경우이다.
즉, 중심이 도형에 위치해 있지 않고 도형 밖에 위치해 있는 경우가 되겠다.
이럴때는 도형 밖에 중심을 잡아야지 하는 생각을 가지고 차근히 중심을 찾아야한다.
이 그림에서 보듯이
우리가 처음 찾아야 하는 부분이
1. 중심선을 찾아라.
중심선을 찾는 것이다. 45도 사선을 지나는 모든 중심선을 잡아서 연결을 해주자.
그럼 도형 안이든 도형 밖이든 원의 중심선을 찾을 수 있을 것이다.
2. 사선이 있으면 사선과 중심선이 만나는 지점을 찾자.
도형에서 중심선이 있고 사선이 있다면 사선을 연장을 하든 자르기를 하든 중심선과 만나는 부분을 확인해야한다.
그 이유는 바로 그 점이 기울어져 있는 사선 단면의 타원의 중심이 되는 경우이기 때문이다.
다음 그림을 보고 확인해보자
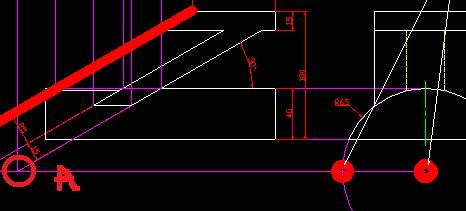
그림에서 A부분의 원에 오른쪽 원의 중심선과 사선의 연장선이 만나는 지점을 확인할 수 있다.
이렇게 찾아주면 일단 준비는 끝난샘이다.
3. 원의 사분점(쿼터점)의 연장선을 확인해라.
우선 원의 중심선과 사선의 연장선으로 깍여진 부분의 중심점을 찾을 수 있었다 하지만 깍여서 기울여져 있는 부분의 원의 폭을 알 수는 없는 노릇이다. 그래서 이 폭을 알기 위해서 쿼터점을 잡고 연장을 해주어야한다.
즉, 이 쿼터점이 타원의 폭이 되는 것이다.
원통에서도 사분점을 찾고 기울여져 있는 원에서도 사분점을 꼭 확인해서 연장을 해보자.
그럼 타원의 장축과 단축을 알 수 있게 될 것이다.
++
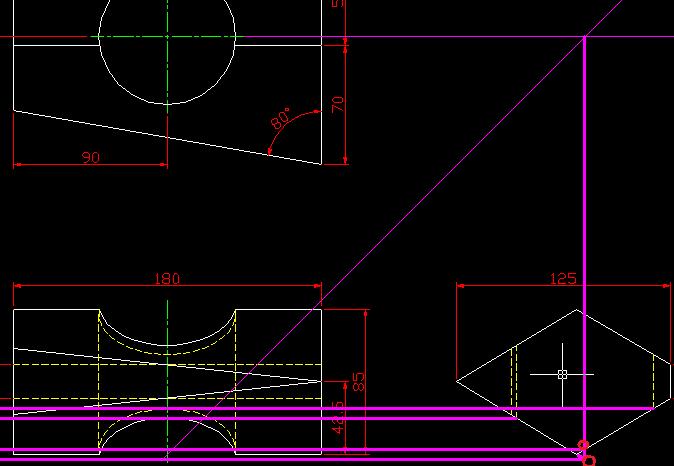
다음 그림에서 사선과 원의 포인트를 확인해보자.
빨간색 동그라미를 주의 깊게 생각해야한다.
'FA System > 투상' 카테고리의 다른 글
| [투상] 원통에서 나타나는 타원 (0) | 2008.06.30 |
|---|---|
| [투상] 기울여진 면이 잘려나간 부분의 사선 표현 (2) | 2008.06.24 |
| [투상] 곡면과 곡면의 경계면 그리기 (0) | 2008.06.22 |
